| Ano de escolaridade: |
|
Disciplina/área curricular: |
|
| Domínio/Tema: |
|
|
| Prova/Ano escolar: |
|
|
| Palavras-chave: |
|
|
Apresentação do Item (Clique aqui para aceder à prova em PDF): |
|
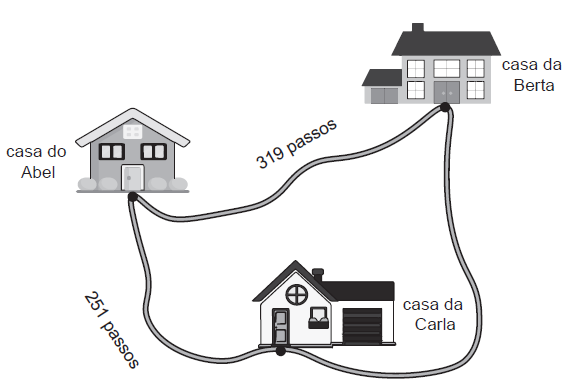
O Abel saiu de casa, foi à casa da Berta, depois passou pela casa da Carla e seguiu para a sua casa, dando 870 passos, no total. O percurso está representado na figura.
Quantos passos deu o Abel entre a casa da Berta e a casa da Carla? Mostra como chegaste à tua resposta. |
| Características do Item | ||
| Tipologia: |
|
|
| Formato: |
|
|
| Tipo de suportes: |
|
|
| Nível de complexidade cognitiva*: |
|
|
| Dados estatísticos | |||
| Percentagem de acerto: |
|
||
| Grau de dificuldade*: |
|
||
| Objetivos do item: o que se pretende avaliar e sua relação com as AE e o PA | |
|
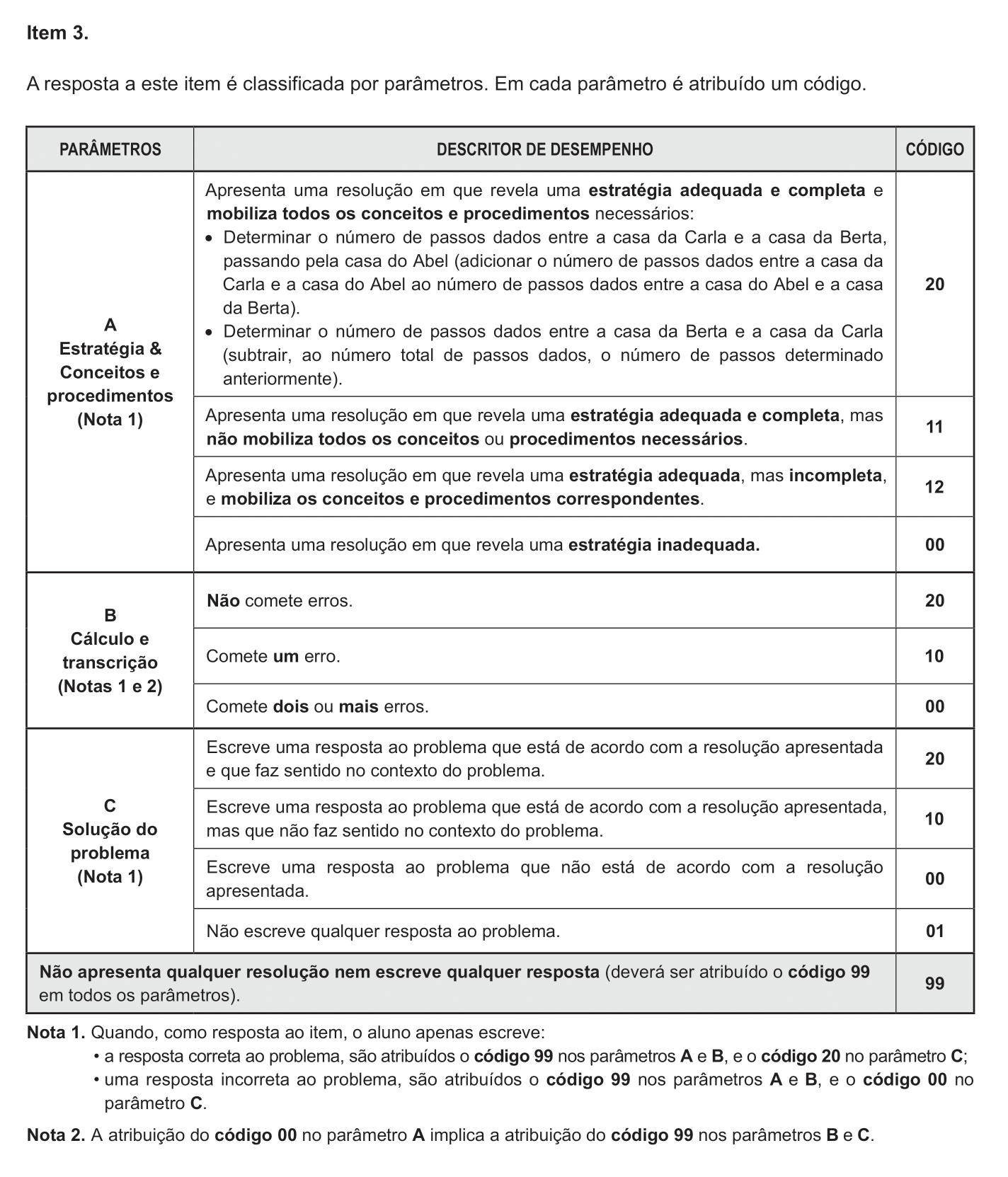
| Critérios de classificação (Clique aqui para aceder aos critérios de classificação em PDF): | |
|
| Exemplos de didáticas e situações de aprendizagem a que os alunos poderiam ser sujeitos para responder corretamente ao item: | ||
|